1527: 最短路径
[Creator : ]
Description
在一个无限大的二维网格里,有三个格子:A,B,F。你要从A格子出发,目标是到达B格子,前提是:
1、每一步可以走到当前格子的上、下、左、右四个相邻的格子之一。
2、任何时候都不能进入F格子。
问在满足上述条件下,从A格子到B格子最少要走多少步?
Input
多组测试数据。
第一行,一个整数t,表示有t组测试数据。1<=t<=10000。
每组测试格式如下:
第1行, 两个整数:x[A]和y[A],表示格子A的坐标。 1<=x[A],y[A]<=1000。
第2行, 两个整数:x[B]和y[B],表示格子B的坐标。 1<=x[B],y[B]<=1000。
第3行, 两个整数:x[F]和y[F],表示格子F的坐标。 1<=x[F],y[F]<=1000。
格子A,B,F不会相同。
Output
共t行,每行一个整数。
Sample Input Copy
2
1 1
3 3
2 2
2 5
2 1
2 3
Sample Output Copy
4
6
HINT
第一组测试数据的其中一种最短走法:
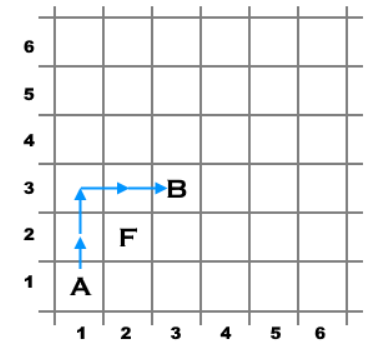
第二组测试数据的最短一种走法:
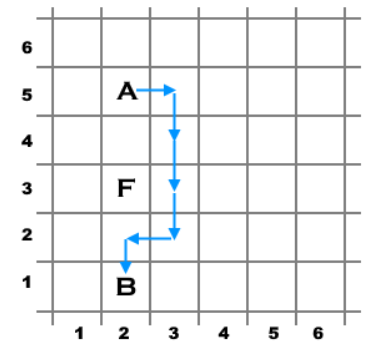

第二组测试数据的最短一种走法:
